Making sense of Redis’ SCAN cursor
In this blog post, I try to figure out why Redis returns those seemingly arbitrary numbers for SCAN commands.

Why Redis returns those seemingly random numbers
At Q42 we build and maintain the Cloud of the Philips Hue lighting system. If you turn on your lights via Google Home or Alexa, this passes through the Hue Cloud. Sometimes it is necessary to perform some task for every bridge connected to the cluster (example task: synchronizing which bridges are connected to which cluster). We keep a record in Redis for every connected Hue Bridge, and it contains the address of the backend server the bridge is connected to. If we want to get the IDs of all connected bridges, we can traverse all keys in Redis. For this, Redis has two commands:
KEYS pattern(docs), returns all matching keys at once. This block the Redis server and you should ⚠️️️ NEVER DO THIS IN PRODUCTION ⚠️.SCAN cursor [MATCH pattern] [COUNT count](docs), returnscountkeys (default = 10) and a seemingly random ‘cursor’ so you can get the next page of keys in a next request. This prevents blocking the server for too long.
This article is about that SCAN-command’s cursor.
Have you ever wondered what the cursor value means that Redis returns for SCAN commands? No? Read on! I set out to make sense of these seemingly arbitrary numbers.
SCAN cursor MATCH prefix:* COUNT 1000
Some time ago I was reading a StackOverflow article, that linked the documentation inside the Redis SCAN implementation. At the time, I only quickly skimmed the text. I remember thinking that it should be possible to come up with an estimate of how far along the SCAN is.
Today I ‘cracked’ the algorithm. It is not really that much of an achievement, given it is thoroughly documented, but figuring it out without the source code documentation still gave me a eureka moment. The result:
-> % node debug-redis-SCAN.js 21
INPUT REVERSE-BITWISE REVERSE VAL % OF 2^21-1 (111111…)
858947 11000010110110001011 1596182 76.11%
1885267 110010100010001100111 1655911 78.96%
2008915 110010101110010101111 1662127 79.25%
1566163 110010111010011111101 1668349 79.55%
962867 11001100100011010111 1675694 79.90%
307123 1100110111110101001 1687204 80.45%
784031 11111001011011111101 2043386 97.43%
The table says it all if you look closely, but might seem a bit cryptic at first. I’ll explain what Redis does. Spoiler: it is as elegant as it is simple.
Suppose you have N keys, then Redis has reserved a hash-table that is a bit bigger than N, namely it reserves a power of 2 such that 2^X > N (read: such that it fits). In above result the X is 21, so the maximum number of ‘buckets’ the table fits is 2.097.151. Once you use more keys than that, Redis will double the table, more on that later. The minimal binary index of that table is `00000…` and the maximum is `11111…` (with N bits).
If you SCAN, you give it a number where to start, which defaults to 0. Redis will take this number, and revert the bits. Then it will read the keys at that index, increment the index, and loop, until the COUNT indexes have been tried. Suppose your table can hold 8 items (X=3, 2³=16). Lets see what happens if we SCAN with a COUNT of 1, Redis would use these values:
COMMAND BITS SWAPPED NEXT SWAPPED CURSOR RETURNED
SCAN 0 __0 000 001 100 4
SCAN 4 100 001 010 010 2
SCAN 2 _10 010 011 110 6
SCAN 6 110 011 100 001 1
SCAN 1 __1 100 101 101 5
SCAN 5 101 101 110 011 3
SCAN 3 _11 110 111 111 7
SCAN 7 111 111 000 000 0
‘Rehashing’
Here, we increase the cursor with 1 every time, by using COUNT 1. If we would instead use a larger COUNT, then Redis would scan the range of keys that are inside the `[START…START+COUNT]` range. Because it swaps the bit order, it can ‘survive’ situations where the table size is doubled/quadrupled. Example when using COUNT 2:
# no resize
COMMAND BITS SWAPPED +1 +2 SWAPPED CURSOR RETURNED
SCAN 0 __0 000 001 010 010 2
SCAN 2 _10 010 011 100 001 1
vs
# with resize
COMMAND BITS SWAPPED +1 +2 SWAPPED CURSOR RETURNED
SCAN 0 __0 000 001 010 010 2
====== table resizes to X=4 =========================
SCAN 2 __10 0100 0101 0110 0110 6
SCAN 6 _110 0110 0111 1000 0001 1
As you scan see from this demo, it doesn’t matter that the table resizes half-way the SCAN: it still reaches cursor 1, it only takes 1 extra iteration.
Ok, great. But how does this ensure we get every element at least once? Because when the table is resized, the hashing is ‘stable’. So a key that is stored at index 001 with x=3, will be stored at 0010 or 0011 with x=4. Important: the key keeps the prefix 001! And since we’re using this bit-ordering to walk through all keys, we’ll never miss a key when the table is rehashed.
Since a picture says more than a thousand words, here is a picture of what happens when we resize a x=2 table to x=4. Say we just got `[KEY2, KEY3]` and cursor 2 from Redis. If we would continue, we would get KEY1. But what happens if KEY5 is inserted first, and Redis rehashes: if we continue after the rehashing, we will get [KEY5] and cursor 6, and we’ll get [KEY1] the time after.
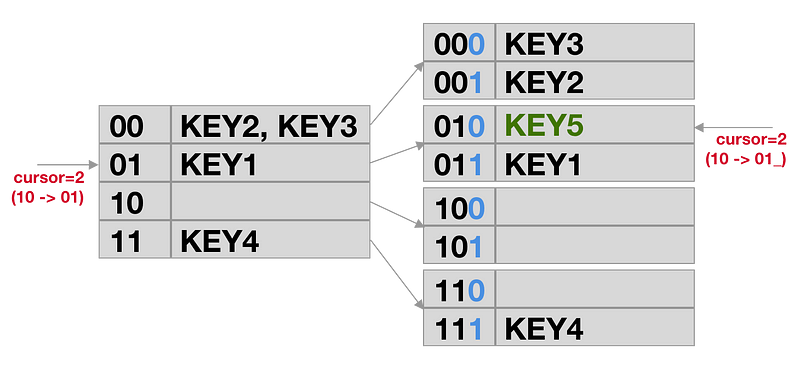
If the table doubles, every row is ‘split’ and the existing cursors out in the client applications will point at the first of the 2 new rows.
Exploiting this knowledge
Given this knowledge, we can now do more stuff than we could before. For example:
- if we know the approximate size of the table, we can guess X
- given X, we can generate a cursor at approximate percentages (say: 0% & 50%) and parallelize the iteration
- given a cursor and knowing X we can estimate how far along we are
In a follow-up article we’ll dive into how to do these things!
References
- During the process of writing this blog post, I found the following article, which explains how SCAN works in more detail: https://medium.freecodecamp.org/redis-hash-table-scan-explained-537cc8bb9f52
- Source of SCAN: https://github.com/antirez/redis/blob/fd0ee469ab165d0e005e9fe1fca1c4f5c604cd56/src/dict.c#L778-L861
Check out our job vacancies (in Dutch) at werkenbij.q42.nl!
